 |
 |
 |
 |
 |
 |
 |
|---|
Как сбит MH17: гражданское расследование |
Привет, Гость! Войдите или зарегистрируйтесь.
Вы здесь » Как сбит MH17: гражданское расследование » Математическое и компьютерное моделирование » Математическое моделирование траектории падения центроплана #2
На картинке в клеточку запредельные скорости, этого неможет быть.
Если сбросить балванку весом 250 тонн с высоты 10000 метров без крылошек под углом к горизонту 70 градусов. то максимальная скорость у земли будет 460 м/сек. http://forumupload.ru/uploads/0016/23/c6/51/804874.png
Предыдущая часть темы: Математическое моделирование траектории падения центроплана
Так как скорость полотен на разных участках высоты была разной, то определение BC по формуле BC=(V^2*ro)/(2*g) верно только для определенной плотности.
Более реальный метод определение среднего BC по локусу, если полотно выпало на эшелоне, то ВС соответствующего полотна можно определить так как показано на картинке.
Акулич так же как Басар рекламирует свою картинку.
Акулич, как может улететь текстиль на такое расстояние с баллистическими коэффициентами (ВС) 0,252 или 0,363?
Как назвать Акулича? Простачком, врунишкой, фантазером?
Акулич так же как Басар рекламирует свою картинку.
Акулич, как может улететь текстиль на такое расстояние с баллистическими коэффициентами (ВС) 0,252 или 0,363?
Как назвать Акулича? Простачком, врунишкой, фантазером?
Как ВС полотен могут отличаться нв треть и при этом падать с 10 км практически в одну точку? Прежде, чем 3.14здеть о "БК" полотен и демонстрировать свою тупизну ссылки бы проштудировал. Ссылка
Как ВС полотен могут отличаться нв треть и при этом падать с 10 км практически в одну точку? Прежде, чем 3.14здеть о "БК" полотен и демонстрировать свою тупизну ссылки бы проштудировал. Ссылка
Тебе был задан конкретный вопрос. Акулич, как может улететь текстиль на такое расстояние с баллистическими коэффициентами (ВС) 0,252 или 0,363?
DSB же не с потолка взяли ВС 0,252 или 0,363. Правильно? Поэтому ты свое творчество с картинкой как у басара проверь, построй траекторию с ВС равной 0,252 или 0,363.
Если Акулич ты не построишь траекторию текстиля с ВС равной 0,252 или 0,363, то ты будешь самым натуральным пропиз.дунчиком по версии неантихриста.
Надеюсь ты меня понял?. Прежде, чем 3.14здеть, вначале построй траекторию текстиля, так как я тебе сказал.
Прежде, чем 3.14здеть, вначале построй траекторию текстиля, так как я тебе сказал.
Дядя, ты дурак? Ты что не понимаешь написанного? Для построенния траектории падения полотен никакой БК не нужен в принципе. Вертикальная составляющая скорости полотен на любой высоте определятся из отношения скоростей. Мало того, действующее на полотна лобовое сопротивление в разы меньше сопротивления силы трения действующее вдоль полотен, поэтому характеристики падения полотен должны определяться из условий движения тел в ламинарном потоке. Указанные ДСБ ВК полотен не могут соответствовать действительным значением ( как и скорости падения)хотя бы потому, что отличаются на треть. И какие это БК: в вертикальном или горизонтальном направлении?
Вообщем изучи вышеуказанные ссылки.
Дядя, ты дурак? Ты что не понимаешь написанного? Для построенния траектории падения полотен никакой БК не нужен в принципе. Вертикальная составляющая скорости полотен на любой высоте определятся из отношения скоростей. Мало того, действующее на полотна лобовое сопротивление в разы меньше сопротивления силы трения действующее вдоль полотен, поэтому характеристики падения полотен должны определяться из условий движения тел в ламинарном потоке. Указанные ДСБ ВК полотен не могут соответствовать действительным значением ( как и скорости падения)хотя бы потому, что отличаются на треть. И какие это БК: в вертикальном или горизонтальном направлении?
Вообщем изучи вышеуказанные ссылки.
Ну как я и ожидал ты самый что ни наесть пропиз.дунчик. Где этот 3,14здабол неантихрест, пусть тебе на лоб поставит клеймо - пропиз.дунчик.
читаем отчет DSB:
Calculation of the drop speed was done using six images. This yielded a result of 4.1 metres/second. For calculation a range of drop speeds were taken between 4 and 5.5 metres per second which resulted in a Ballistic Coefficient between 0.252 and 0.363.
Расчет скорости падения проводился с использованием шести изображений. Это дало результат 4,1 метра в секунду. Для расчета был взят диапазон скоростей падения от 4 до 5,5 метров в секунду, что привело к баллистическому коэффициенту от 0,252 до 0,363.
Акулич ты видишь там баллистические коэффициенты 0,252 и 0,363? Надеюсь видишь!
Акулич написал:
Для построенния траектории падения полотен никакой БК не нужен в принципе.
Не 3,14зди Акулич - пропиз.дунчик тебе DSB дало ВС, вот и извольте пропиз.дунчик построить траектории с ВС равными 0,252 и 0,363! 
Расчет скорости падения проводился с использованием шести изображений. Это дало результат 4,1 метра в секунду. Для расчета был взят диапазон скоростей падения от 4 до 5,5 метров в секунду, что привело к баллистическому коэффициенту от 0,252 до 0,363.
Ты продолжаешь жевать то, что я ... "пропустил" через себя более двух лет назад еще на смоленском. Приятного аппетита. 
Ты продолжаешь жевать то, что я ... "пропустил" через себя более двух лет назад еще на смоленском. Приятного аппетита.
Мне безразлично, что ты там через себя пропускал. Кстати представь, что ты сбрасываешь шарик с ВС 0,252 и 0,363. Или ты просто не в состоянии построить траектории полотен с ВС от DSB? Так и скажи, что пропиз.дунчик не может построить траектории материальной точки.
Программа Усчена не оперирует с такими величинами ВС?
Кстати представь, что ты сбрасываешь шарик с ВС 0,252 и 0,363.
Дурачок, "шарик" имеет ВС одинаковый во всех направлениях а падающее полотно совершенно разные в горизонтальном и вертикальном направлениях. Как можно сравнивать ВС "шарика" и полотен? 
Кроме того ВК нужен при определении характеристик движения тел, для которых основной вид сопротивления- лобовое. В случае полотен основной вид сопротиления - это силы трения по всей длине полотен. Никакой ВК в формулу определения силы сопротивления в этом случае вообще не входит.
Кстати ВС для материальной точки несуществует, поскольку зависит от размеров и формы, которых у мат. точки нет по определению. О чем тебе сообщалось не менее года назад.
Ну что же ты такой тупой....
Отредактировано Акулич (2021-07-23 00:14:04)
В случае полотен основной вид сопротиления - это силы трения по всей длине полотен
Да, это скорее парашютирование, а не падение.
Дурачок, "шарик" имеет ВС одинаковый во всех направлениях а падающее полотно совершенно разные в горизонтальном и вертикальном направлениях.
А пластина имеет по всем направления одинаковые величины Сх, массы и миделя?
Глупенький Акулич, нет же, пластина не может иметь одинаковые величины Сх, массы и миделя по все направлениям, но для расчета траектории падения пластины берутся средние величины, такие же средние величины берутся и для вращающихся и кувыркающихся тел.
То же самое для полотен берется средний ВС.
Глупенький Акулич, ты что DSB считаешь необразованными лохами. а себя академиком? Ты Акулич не академик, а пропиз.дунчик по версии неантихриста.
Хорошо если тебя не устраивает шарик, то построй траекторию падения пластины с средним БК равному 0,252 или 0,363. Не уверен, что ты сможешь построить траекторию падения пластины так как ты кроме бла-бла ни на что неспособен. Докажи что я ошибаюсь и построй траекторию.
Кстати ВС для материальной точки несуществует, поскольку зависит от размеров и формы, которых у мат. точки нет по определению. О чем тебе сообщалось не менее года назад.
Дурачок мы же с помощью программы баллистических траекторий не "сбрасываем" 3D объект. а сбрасываем (ну хорошо уговорил) "геометрическую точку", задавая ей параметры в том числе и ВС. Кстати DSB строит линию локуса из множества точек, каждая точка Локуса это "геометрическая точка" которую сбрасывают с высоты.
Отредактировано oper (2021-07-23 00:56:07)
То же самое для полотен берется средний ВС.
ДБ, средний БК для полотен - это как средняя температура по больнице . Если взять некий средний ВС (одинаковый по горизонтальной и вертикальной оси) , то это значило бы , что силы сопртивления движению тоже были бы одинаковы при одинаковых скоростях воздушного потока . Это абсурд.
Ты что не способен воспринимать новую для тебя информацию о особенностят падения полотен?
А пластина имеет по всем направления одинаковые величины Сх, массы и миделя?
Глупенький Акулич, нет же, пластина не может иметь одинаковые величины Сх, массы и миделя по все направлениям, но для расчета траектории падения пластины берутся средние величины, такие же средние величины берутся и для вращающихся и кувыркающихся тел.
Разве полотна "вращаются и кувыркаются"? 
Кроме того, про средний БК для "вращающихся и кувыркающихся плостин" тебе кто то наврал. 
Отредактировано Акулич (2021-07-23 01:16:21)
сбрасываем (ну хорошо уговорил) "геометрическую точку",
Новое слово в геометрии? Г.Т. - обладает площадью, массой , формой? Ну ты силен....
ДБ, средний БК для полотен - это как средняя температура по больнице . Если взять некий средний ВС (одинаковый по горизонтальной и вертикальной оси) , то это значило бы , что силы сопртивления движению тоже были бы одинаковы при одинаковых скоростях воздушного потока . Это абсурд.
Ты что не способен воспринимать новую для тебя информацию о особенностят падения полотен?
Вот опять Акулич ДБ пытается унизить экспертов DSB, тем самым еще больше подтверждая свою сущность пропиз.дунчика (по версии неантихриста). Эксперты DSB рассчитали ВС, а ты "академик" считаешь, что они дураки.
Акулич ДБ с помощью программы баллистических траекторий "ТАР" DSB моделировала падение 14 фрагментов, большинство которых части фюзеляжа, которые "плоские" и падая вращаются и кувыркаются , в том числе находила и ВС для полотен текстиля.
Ты просто не в состоянии получить координаты с помощью диф. уравнений. а то бы на счетах за 6-7 лет уже бы насчитал. Программы же у тебя нет, а Усчена прога с такими маленькими величинами ВС считает херню. Да Акулич?
Кроме того, про средний БК для "вращающихся и кувыркающихся плостин" тебе кто то наврал.
Серьезно? Тогда вначале расскажи как у куска фюзеляжа определяют мидель и Сх? Неизвестно же какое положение он займет при падении чтобы точно определить мидель и Сх, а значит берется среднее значение, тоже самое касается и вращающихся тел у которых меняются мидель и Сх, соответственно и берутся средние значения, а значит и у БК среднее значение.
Новое слово в геометрии? Г.Т. - обладает площадью, массой , формой? Ну ты силен....
Так ты же считаешь, что нельзя говорить материальная точка при расчете баллистических траекторий, вот и приходится брать в кавычки новые названия, чтобы до тебя дошло что "сбрасываются" с высоты не 3D объекты, а "точки" с массой, миделем и Сх. Скажем так "точка" имеет свойства - масса, мидель и Сх.
Отредактировано oper (2021-07-23 02:43:39)
Очень удивительно, что за 6-7 лет Акулич так и не понял, что все траектории падения построены для материальных точек, чтобы Акулич как то это понял пришлось вводить новые термины и брать их в кавычки.
В отчете представлены уравнения для построения траекторий падения материальных точек, именно используя такого типа уравнения и был построен ЛОКУС DSB.
Кроме массы, ускорения и скорости, в уравнении есть коэффициенты, это не означает что мы присваиваем величины коэффициентов материальным точкам.
Акулич вначале играет в дурочка, а затем с"умным" видом пишет - "Новое слово в геометрии? Г.Т. - обладает площадью, массой , формой? Ну ты силен....", умышленно не замечая кавычки ("геометрическая точка" или просто "точка").
Почему академик Украинец Акулич, который предоставил информацию в отчете по падению полотен, заткнул все свои отверстия - чего он обосрался..
Акулич винтик пропи.дунчик из пропаганд-машины Украины.
Ему же надо просто взять подставить БК 0,252 в программу и проверить свои фантазии с моделированием DSB, а так как он ноль, то не может проверить свои фантазии и поэтому то жидко обосрался...
А почему ты решил, что он "0"
А что разве невидно? Акулич самый натуральный 0.
Винтик пропи.дунчик с восьмилетним образованием выдает себя за академика, он решил поспорить с профессионалами DSB, но не может построить траекторию падения полотен с БК 0,252 или 0,363. Ничего не стоит ему признаться о своем образовании, так нет хитрожопый "академик" неустанно твердит - ненужны БК, я и без них справляюсь.
Расстояние по прямой 3389 метров.
На карте найдем текстиль, который находится на самом небольшом расстоянии от трассы МН17 и от этой метки построим окружность с радиусом 3389 метров. и найдем точку пересечение окружности с курсом 118 градусов МН17. Эта точка пересечения почти совпадает с точкой LFDR.
Это означает Акулич считает, что текстиль начал падение из точки LFDR.
На самом деле расстояние по прямой совсем другое и оно легко находится с помощью локуса 10058-252-118-0.
И соответственно с помощью программы можно найти вертикальную скорость падения и БК текстиля. 
Итого получается моделирование у Акулича неверное, текстиль не мог начать падение из точки LFDR. Акуличу вначале надо найти откуда начал падать текстиль и из этой точки и начать строить траекторию падения, но для этого надо использовать программу или иметь знание не с 8-ми летним образованием.
Отредактировано oper (2021-07-26 15:53:15)
Дескать скорость ветра не влияет на время падения обломков !!! - это же самый настоящий бред....
Нет это не бред, а законы физики. Ветер не может влиять на время падения (не учитываются восходящие потоки).
Изучай.
Без учета ветра
С учетом ростовского ветра
С учетом ветра со скорость в два раза меньше
Как видите при всех трех вариантах время падения одинаковое.
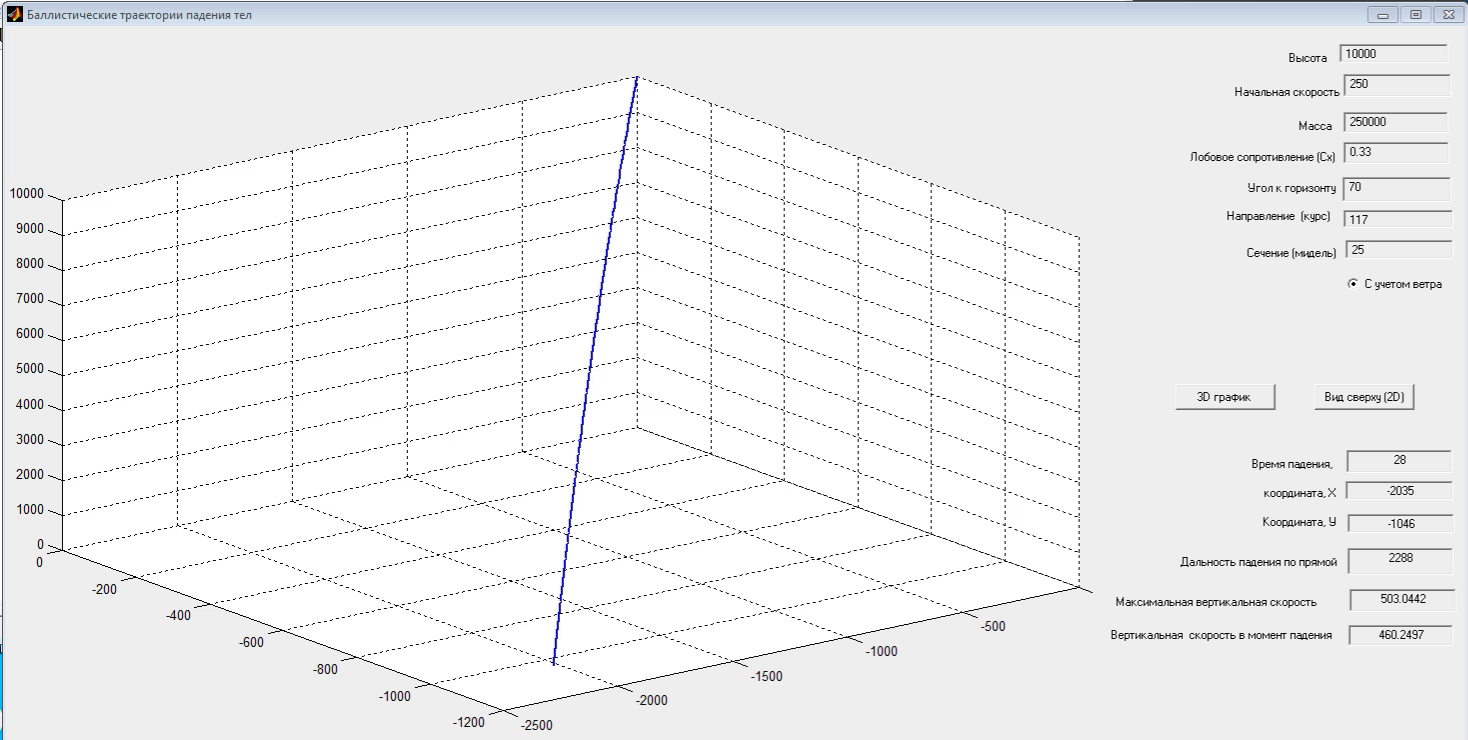
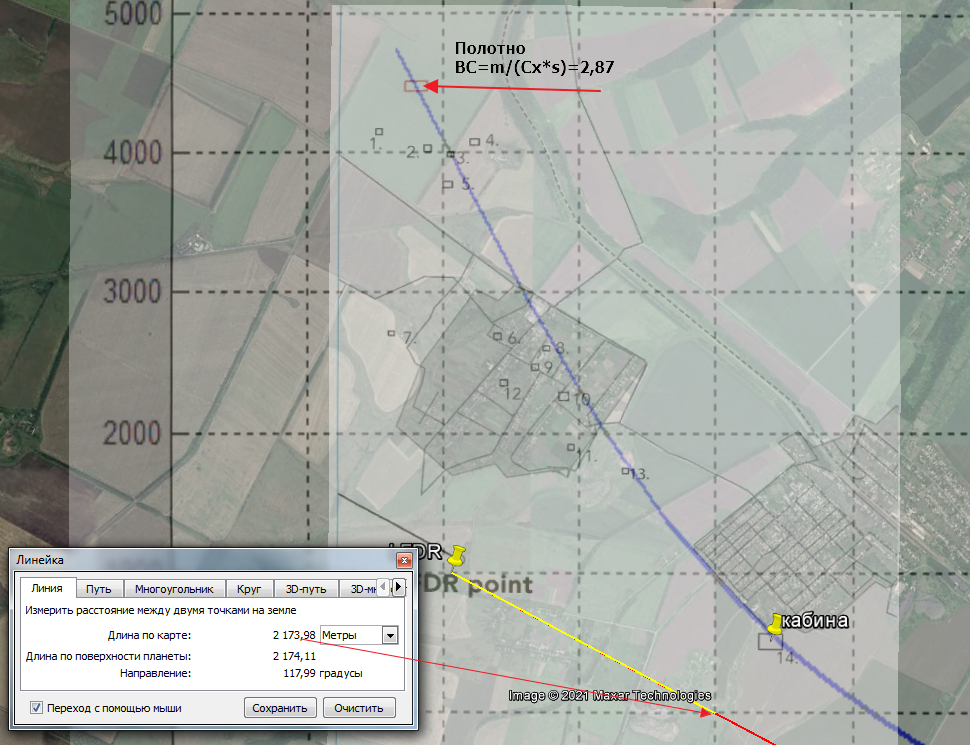
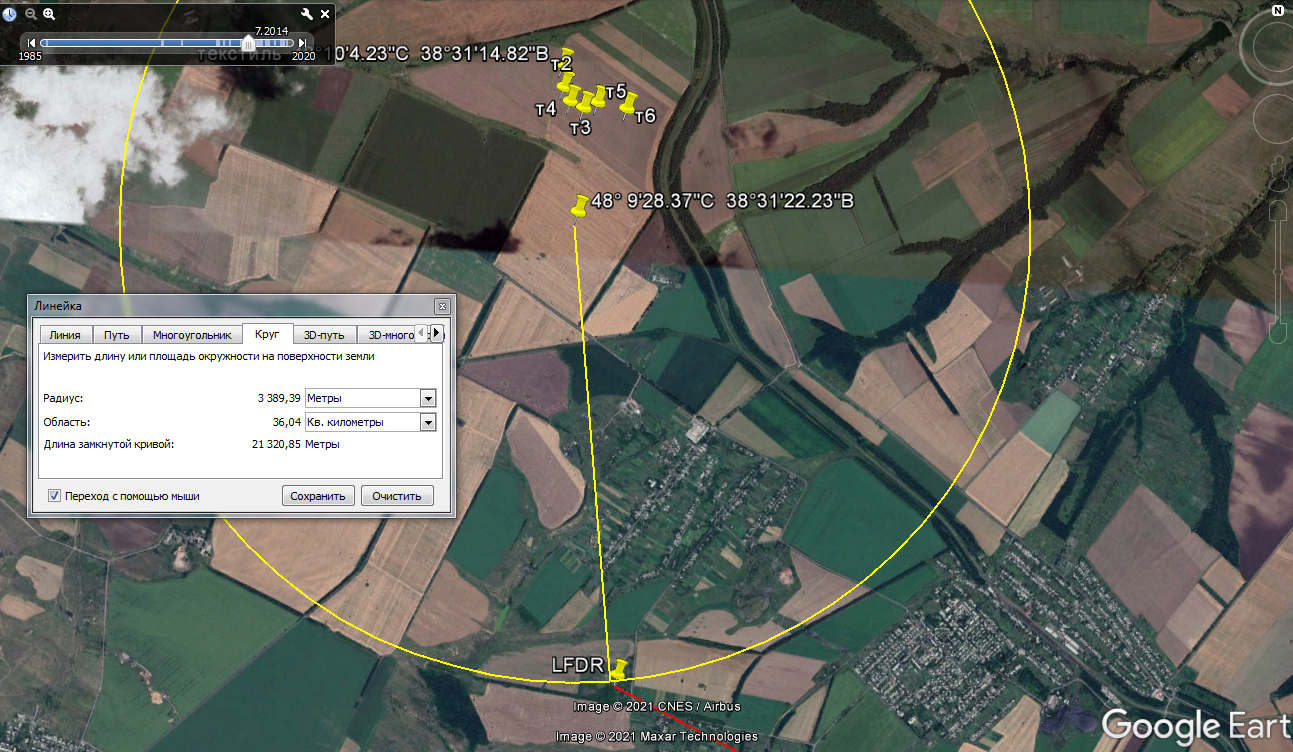
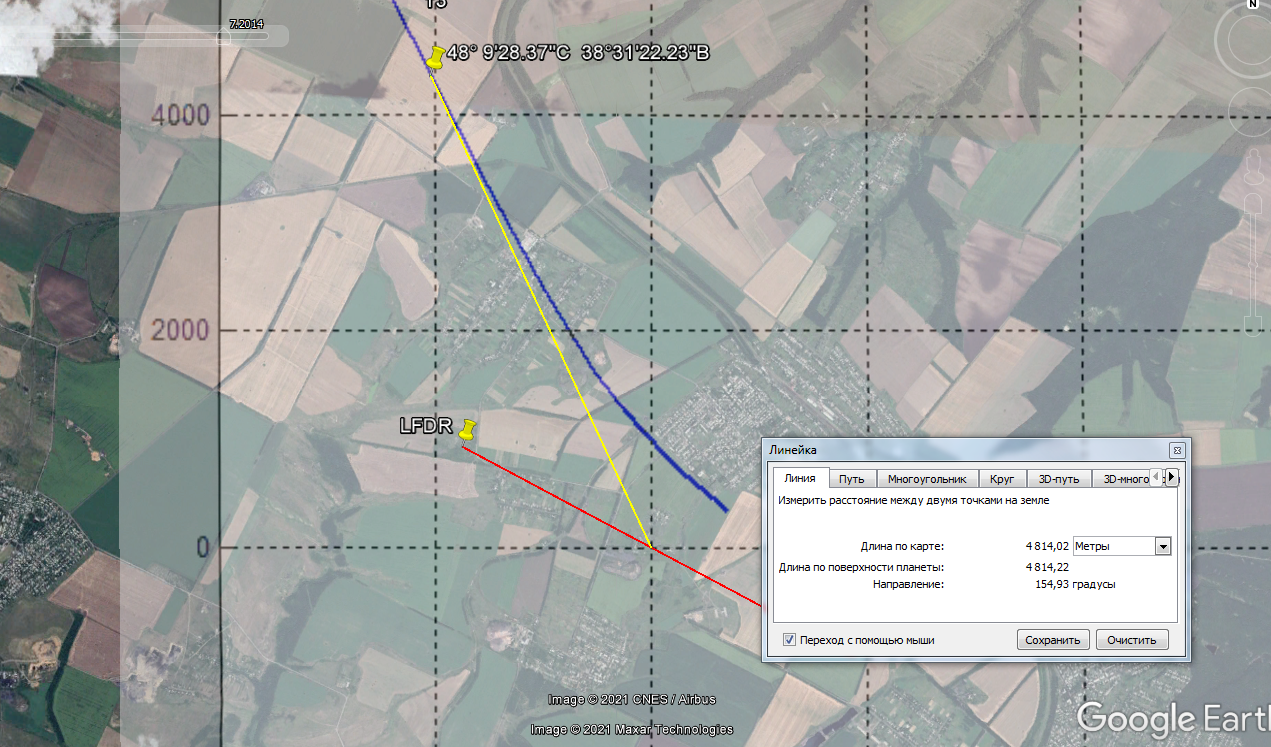
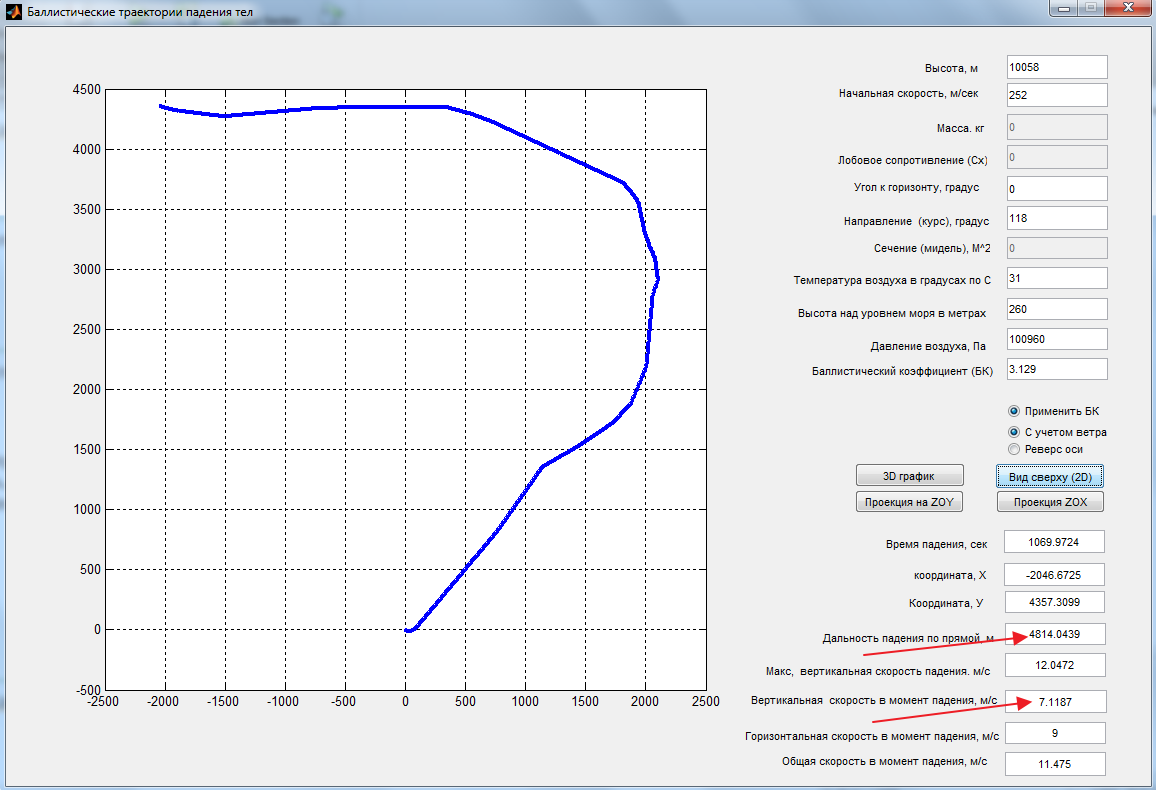
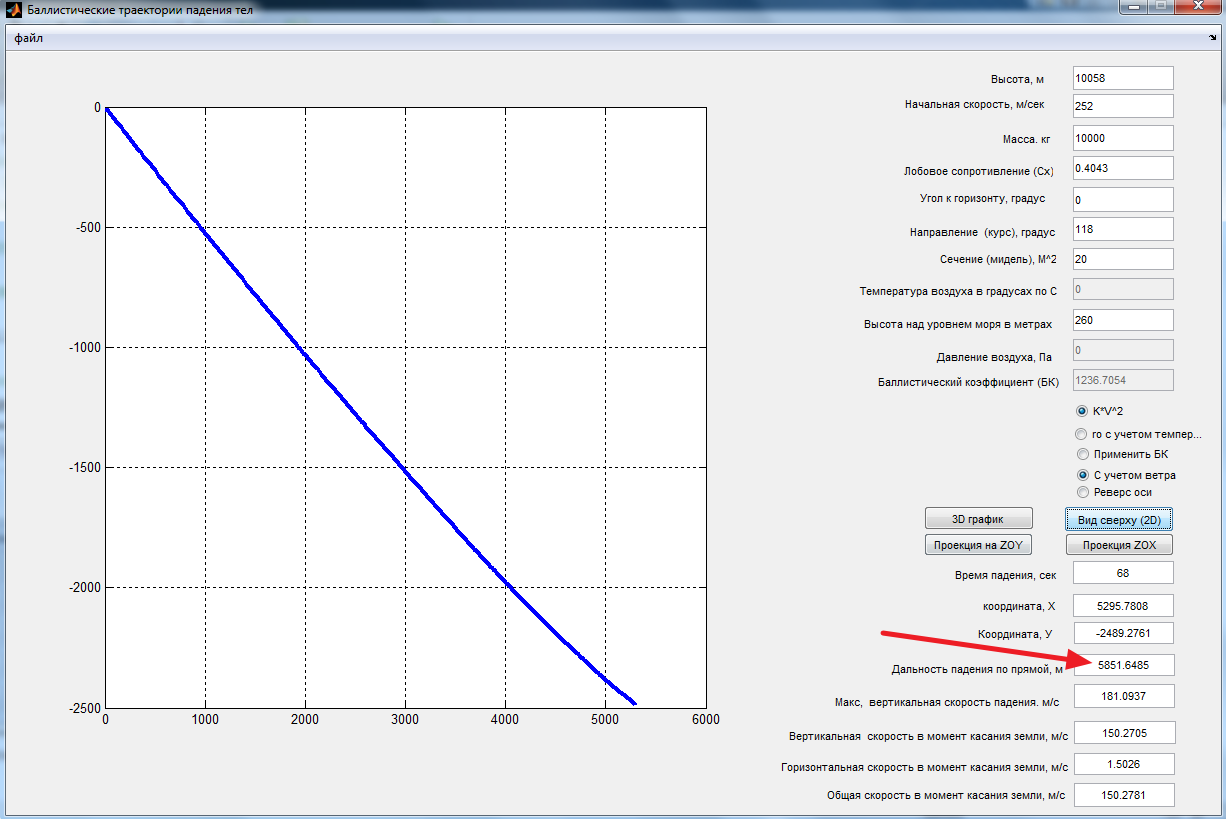
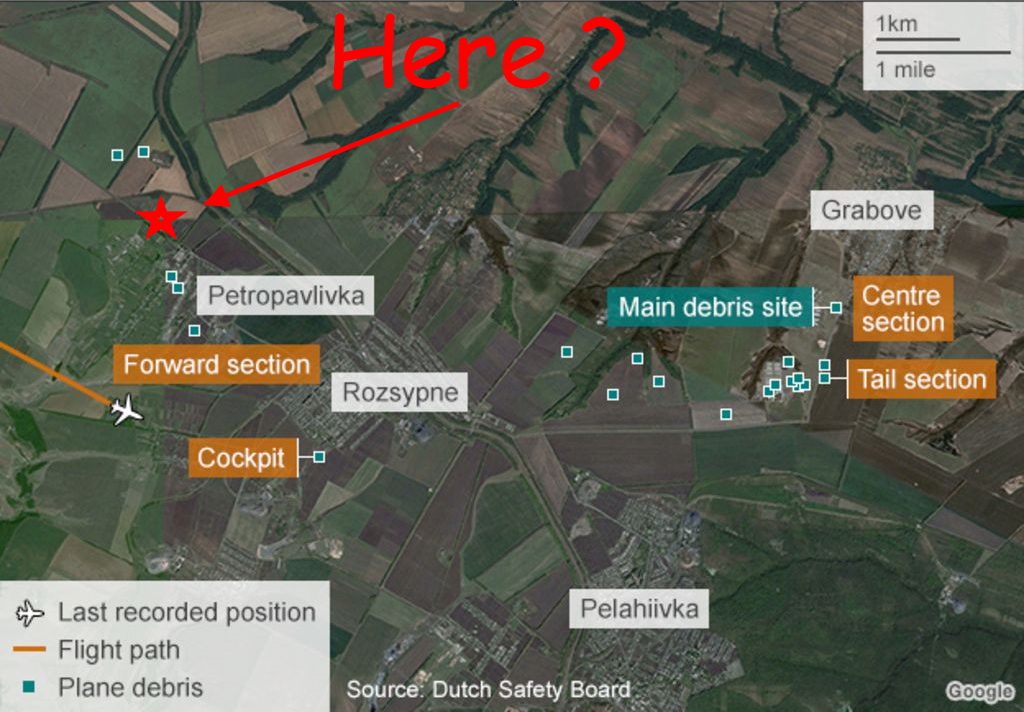
Dutch DSB and JIT have a wrong strike point location of the BUK missile to MW17 airplane. It is about 4-5km too far to Southeast (forwards). It is impossible for a 10 tons´ compact metal debris "package" too fall down from 10000 m height and 250/m speed within 2km´s distance. I can prove with their own information from the "report", that it needs about 6000 m distance to fall down.
https://www.onderzoeksraad.nl/en/media/ … ctief2.pdf
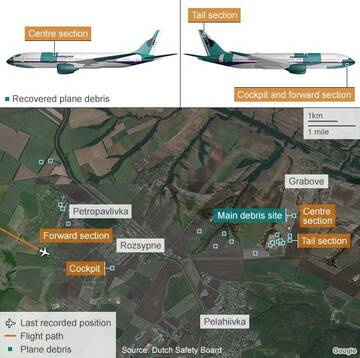
The real strike point is about at the left side of the picture in "height" of the word "Hrabove" (its administration building).
2.10 Wreckage and impact information
2.10.1 Wreckage distribution
Wreckage from flight MH17 was discovered spread over a large area near the towns of Rozsypne and Hrabove in eastern Ukraine. The main wreckage site was located 8.5 km on a bearing of 080° from the last known position of the aircraft in flight. On the accident site, a large amount of photographs was made, which allowed identification of certain aircraft parts, including preliminary assessments of localization and the nature of damage on the fuselage skin and the engines. The aircraft wreckage, identified from the on-site photographs and satellite images, consisted of many large and small pieces distributed over an area of approximately 10 km by 5 km (figure 6). Fuselage pieces, cargo and baggage were scattered throughout the wreckage site. There were many additional unidentified pieces that are not shown in the figure. For easy reference the wreckage site has been divided into sections as shown in
https://www.tiede.fi/comment/3121054#comment-3121054
13:20:05 ... 13:20:06 ELT registered a 2g:n longitudinal acceleration. The ccckpit was loose, disconnected from the fuselage.
https://www.tiede.fi/comment/3127339#comment-3127339
The cockpit has flown 5000 - 6000 m when its drag has been -2g at the disconnection moment
https://en.wikipedia.org/wiki/Drag_(physics)
mdv/dt = mv´(t) = - ρACv²(t)/2 = - cv²(t) = the drag force
v´(t)/v²(t) = - c/m = constant = -2g/vo² = -20ms⁻²/(250ms⁻¹)² = - (3125m)⁻¹ = -k
Integrating implicitely:
-v⁻¹(t) = -k(t - to), where to is integation constant, which gives
v(t) = k⁻¹(t - to)⁻¹
v(0) = 250ms⁻¹ = vo = -k⁻¹to⁻¹, which gives
to = -k⁻¹vo⁻¹ = - vo/(2g) = - 250ms⁻¹(20ms⁻²)⁻¹ = - 12.5s.
The distance d(t) at time t:
d(t) = int v(t)dt = k⁻¹[ln (t - to) - ln (0 - to)] = k⁻¹ ln (1 - t/to) = 3125m ln (1 + t/12.5s)
At the fall the same c/m = k = (3125m)⁻¹ can be used. (It can be regarded to be constant in trajectory direction.)
Now v(0) = 0, and the acceleration downwards dv(t)/dt = -g.
Now
m dv(t)dt = mv´(t) = mg - cv²(t),
v´(t)/(v²(t) - mg/c) = c/m = k, which is taken from the former task.
Let´s define still one coefficient:
k/g = p² = c/(mg), p = sqrt⁻¹(31250) m⁻¹s = 176.8⁻¹m⁻¹s
(m in two meanings: the mass and meter...)
v´(t)/(v²(t) -p⁻²) = gp²:
- p artanh (p v(t)) = (t - t1) gp²,
where t1 = 0 from v(0) = 0.
v(t) = p⁻¹ tanh(gpt) = 176.8ms⁻¹tanh (t /17.68s)
The fall height (from the top)
h(t) = int (v(t))dt = g⁻¹p⁻²ln cosh (gpt) = k⁻¹ln cosh(gpt) = 3125m ln cosh(t/17.68s)
For "larger" x: ln cosh x > x - sqrt2 = x - 0,693.
3125m (t/17.68s - 0.693) = 10000m => t /17.68s = 3.2 + 0.693= 3.893 =>
T = 68.8s IS THA FALL TIME.
In this time the cockpit goes in horisontal direktion distance
d(T) = 3125m ln (1 + 68.8s/12.5s) = 5851 m
***
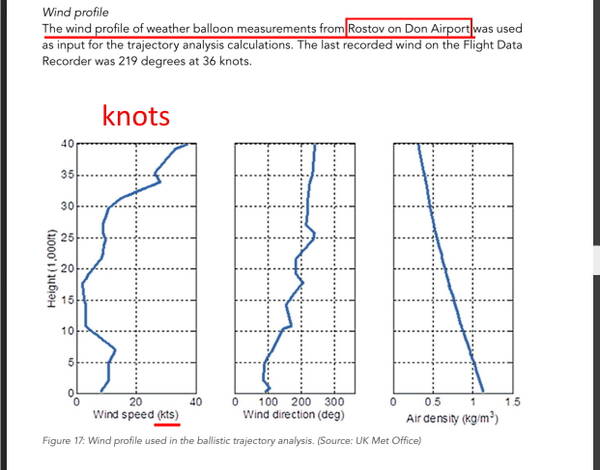
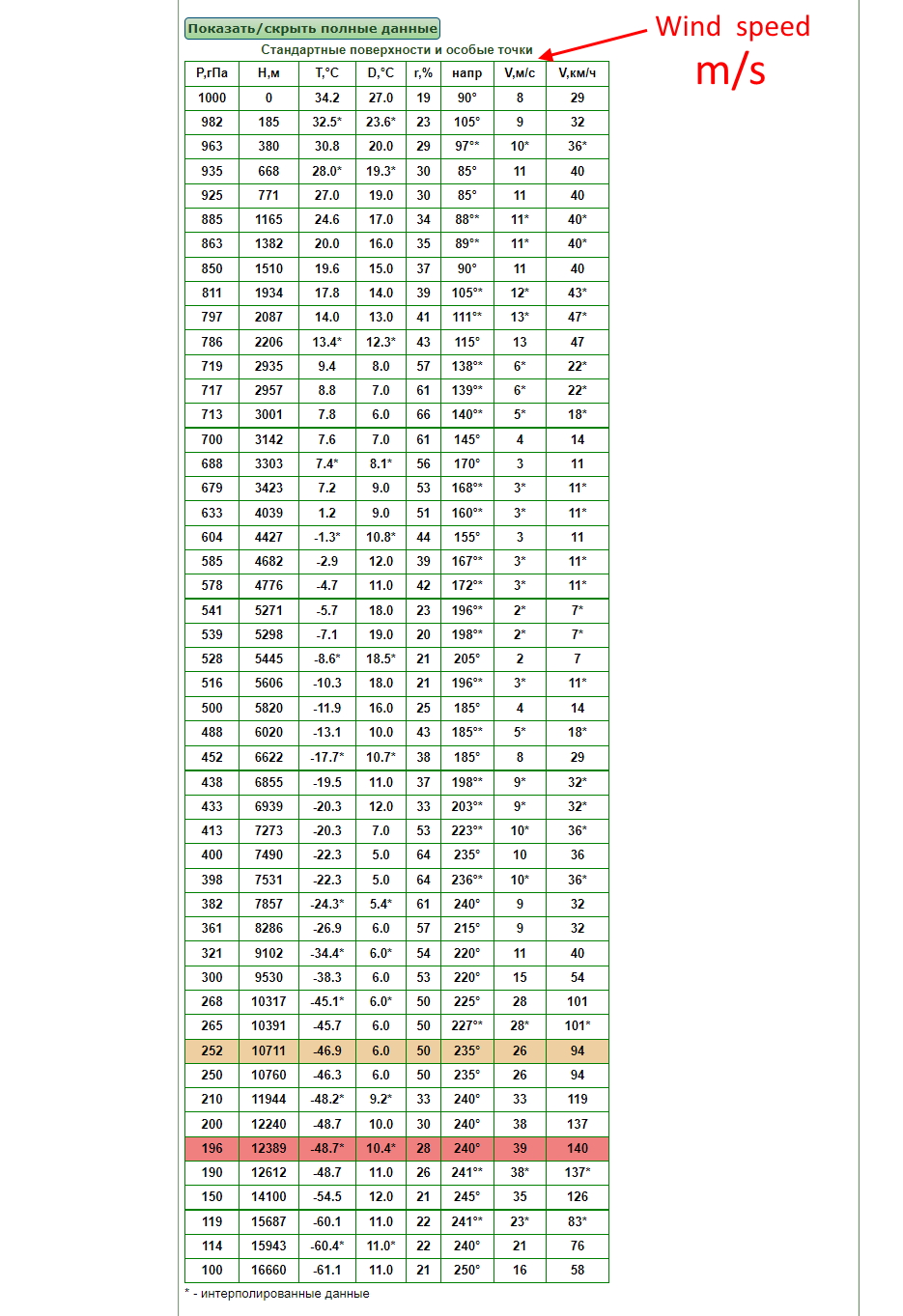
DSB says the wind speed was 18 m/s from direction 210.
The transversal dispalement from wind can also be calculated by drag formula by "changing the drag direction" to positive.
mv´(t) = ρAC(v(t) - v1)²/2 = c(v(t) - v1)², where v1 = 18m/s
v´(t)/(v(t) - v1)²= c/m = constant (from the first task) = 20ms⁻²/(250ms⁻¹)² = (3125m)⁻¹ = k
- (v(t) - v1)⁻¹ = k (t - to)
v(t) = - k⁻¹/(t - to) - v1 = - 3125m/(t - to) + 18.5m/s
v(0) = 0 = 3125m/to + 18.5m/s
=> to = -3125m /18.5ms⁻¹ = - 169 s
v(t) = 18.5m/s - 3125m/(t + 169s)
The speed in horizontal direction at falling point on earth
v(69s) = 18.5m/s - 3125m/(169 + 69)s = 5.4m/s (acceptable),
d(t) = int v(t)dt = t v1 - k⁻¹ [ln(t - to) - ln to] = t v1 - k⁻¹ ln (1 - t/to)
= 69s x 18.5 m/s - 3125m ln (1 + 69/163)
= 1276,5 m - 1069,9 m = 207m FROM WIND.
PS: In this transversal to the trajectory plane direction the projection area A in ρAC = c can be different, for instance double to that in plane normal to trajectory.
If it is double, then k -> 2k = (1562.5m)⁻¹ , ja to -> to/2 = 85.5s.
Then d(T) = 69s x 18.5m/s - 1562.5m ln(1 + 69s/85.5s) = 352m from that same transversal wind 18,5 m/s.
(I have calculated with other means that absolute maximun transversal to the original flight line trasition from maximum wind (about 50 m/s) is about 600 m for the fuselage or cockpit.)
Отредактировано Risto_Koivula,_Tampere (2022-01-06 01:41:41)
d = 3125m ln (1 68.8s/12.5s) = 5851 m
Dutch DSB and JIT have a wrong strike point location of the BUK missile to MW17 airplane.
The real strike point is about at the left side of the picture in "height" of the word "Hrabove" (its administration building).
Spammiro Botti kirjoitti:
Nyt on käynyt ilmi, että me emme tiedä mitään tuulista, koska DSB on fuskannut, ja venäläiset tai donilaiset eivät anna oikeita tietoja, jos heillä sellaisia on, ettei DSB pääse korjaamaan fuskujaan.
https://www.tiede.fi/comment/3129350#comment-3129350
Rostov on Don Airport 17.07.2014 12.00 UTC
https://flymeteo.org/arhiv/2014_07_17_34731.php
mdv/dt = mv´(t) = - ρCv²(t)/2
В уравнении пропущен мидель (A - area).
v - velocity
ρ - air density
Сd - drag coefficient
A - area (midship)
Должно быть так:
mdv/dt = mv´(t) = - (ρ*Cd*A*v²)/2
v´(t)/v²(t) = - c/m = constant = -2g/vo² = -20ms⁻²/(250ms⁻¹)² = - (3125m)⁻¹ = -k
Должно быть так:
- Сd*А/m = constant = -k
В зависимости от величины этого коэффициента к=Сd*А*/m можно получить любое расстояние падения
Обратная величина этого коэффициента 1/к называется баллистический коэффициент, BC=m/(Cd*A).
У нас есть условия падения кокпита (высота, начальная скорость, начальное направление падения и угол наклона к горизонту) и координаты падения кокпита, поэтому любое значение коэффициента к не подойдет. а только то при котором кокпит упадет на место падения реального кокпита.
Отредактировано oper (2021-10-21 16:51:14)
В зависимости от величины этого коэффициента к=Сd*А*/m можно получить любое расстояние падения
У нас есть условия падения кокпита (высота, начальная скорость, начальное направление падения и угол наклона к горизонту) и координаты падения кокпита, поэтому любое значение коэффициента к не подойдет. а только то при котором кокпит упадет на место падения реального кокпита.
Слышь, долбoёб ?
Ты хоть понимаешь что ты пишешь ?
Нахуя ты подгоняешь параметры Кокпита под условие lastFDR - место падения ?
Тебе же человек рассчитал необходимое расстояние траектории падения Кокпита при условии что он отделился на высоте 10 км на скорости 250 метров в секунду
In this time the cockpit goes in horisontal direktion distance
d = 3125m ln (1 68.8s/12.5s) = 5851 m
В этом случае не параметры Кокпита меняются, а точка last FDR сдвигается только лишь для того что бы показать что не только она ЯВЛЯЕТСЯ ФИКТИВНОЙ, но и СТАРТОВЫЕ УСЛОВИЯ ТОЖЕ ФИКТИВНЫЕ. Высота, скорость, направление MH17 являются ФИКТИВНЫМИ и СФАЛЬСИФИЦИРОВАННЫМИ.
Нахуй ты его сбиваешь, программист зачуханый ?
Ты не способен сделать ни одного правильного вывода из результатов моделирования.
Иди сука моделируй падение трёх фрагментов из "Задачи Акулича".
Тетя ты куды пришла, математическое моделирование не для тебя, ты що совсем рехнулась?
Фин такой же грамотей как и ты дурочка. У него тела без размера, а значит невидимки, они вроде падают далеко, но их не видно, так как нет миделя. Он где-то спиз*дел формулы и носится по форумам, нифига не соображая, что на самом деле постит.
Тетя ты куды пришла, математическое моделирование не для тебя, ты що совсем рехнулась?
Фин такой же грамотей как и ты дурочка. У него тела без размера, а значит невидимки, они вроде падают далеко, но их не видно, так как нет миделя. Он где-то спиз*дел формулы и носится по форумам, нифига не соображая, что на самом деле постит.
Тут только один "мастер" пиз*дить формулы - это ты.
Для Кокпита Фин получил почти такой же результат как и Glimmung - 6577 метров необходимые для падения Кокпита при заявленных стартовых условиях.
Иди моделируй три фрагмента из "Задачи Акулича" и не суй в эту тему своё жало - без тебя разберёмся.
Для Кокпита Фин получил почти такой же результат как и Glimmung - 6577 метров необходимые для падения Кокпита при заявленных стартовых условиях.
Значит оба использовали ошибочные уравнения!
"Задачи Акулича" должен решать сам Акулич, для решения этих задач не нужны знания, для того чтобы узнать - больше, меньше или равно надо бросить жребий. Монетку два раза подбрось.
Значит оба использовали ошибочные уравнения!
Иди физику учи, программист обосранный.
Risto_Koivula,_Tampere написал(а):
mdv/dt = mv´(t) = - ρCv²(t)/2
В уравнении пропущен мидель (A - area).
v - velocity
ρ - air density
Сd - drag coefficient
A - area (midship)Должно быть так:
mdv/dt = mv´(t) = - (ρ*Cd*A*v²)/2
Risto_Koivula,_Tampere написал(а):v´(t)/v²(t) = - c/m = constant = -2g/vo² = -20ms⁻²/(250ms⁻¹)² = - (3125m)⁻¹ = -k
Должно быть так:
- Сd*А/m = constant = -kВ зависимости от величины этого коэффициента к=Сd*А*/m можно получить любое расстояние падения
Обратная величина этого коэффициента 1/к называется баллистический коэффициент, BC=m/(Cd*A).
У нас есть условия падения кокпита (высота, начальная скорость, начальное направление падения и угол наклона к горизонту) и координаты падения кокпита, поэтому любое значение коэффициента к не подойдет. а только то при котором кокпит упадет на место падения реального кокпита.
Отредактировано oper (Сегодня 12:51:14)
The measured drag deceleration constant 2.0g ... 2.6g of the cockpit, when it had disconnected fronm fuselage, is taken from DSB "report" data. Measurings on speed in first seconds confirms formula v(t) = 3125m/(t + 12.5s):
0 s 250m/s
1 s 230m/s
2 s 211 m/s
If the drag deceleration had been 2.6 g, then
c/m = 2.6g/vo² =26ms⁻²/(250ms⁻¹)² = (2403m)⁻¹ = -k, and
to = -k⁻¹vo⁻¹ = - vo/(2.6g) = - 250ms⁻¹(26ms⁻²)⁻¹ = -9.6s.
Speed horizontally: v(t) = 2403m /(t + 9.6s),
and transalation horizontally: d(t) = 2403m ln (1 + t/9.6s)
In fall cvonstant p = sqrt⁻¹(2430m x 10m/s²) = 155⁻¹s⁻¹.
Falling speed w(t) = p⁻¹ tanh(gpt) = 155ms⁻¹tanh (t /15.5s),
And falling height (from top): h(t) = k⁻¹ln cosh(gpt) = 2403m ln cosh(t/15.5s) => 2403m (t/15.5s - 0.693)
=> The falling time T: 2403m (T/15.5s - 0.693) = 10000m.
=> T = (10000/2403 + 0.693) 15.5 s = 75 s.
The distace of cockpit from strike D = 2403m ln (1 + 75/9.6) = 5230.
Отредактировано Risto_Koivula,_Tampere (2021-12-21 09:35:48)
Вы здесь » Как сбит MH17: гражданское расследование » Математическое и компьютерное моделирование » Математическое моделирование траектории падения центроплана #2